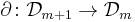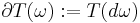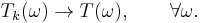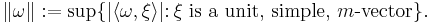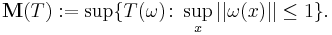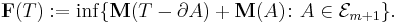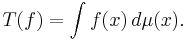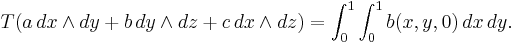Current (mathematics)
In mathematics, more particularly in functional analysis, differential topology, and geometric measure theory, a k-current in the sense of Georges de Rham is a functional on the space of compactly supported differential k-forms, on a smooth manifold M. Formally currents behave like Schwartz distributions on a space of differential forms. In a geometric setting, they can represent integration over a submanifold, generalizing the Dirac delta function, or more generally even directional derivatives of delta functions (multipoles) spread out along subsets of M.
Contents |
Definition
Let 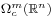 denote the space of smooth m-forms with compact support on
denote the space of smooth m-forms with compact support on 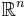 . A current is a linear functional on
. A current is a linear functional on 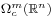 which is continuous in the sense of distributions. Thus a linear functional
which is continuous in the sense of distributions. Thus a linear functional
is an m-current if it is continuous in the following sense: If a sequence 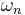 of smooth forms, all supported in the same compact set, is such that all derivatives of all their coefficients tend uniformly to 0 when
of smooth forms, all supported in the same compact set, is such that all derivatives of all their coefficients tend uniformly to 0 when  tends to infinity, then
tends to infinity, then 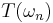 tends to 0.
tends to 0.
The space 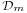 of m-dimensional currents on ℝn is a real vector space with operations defined by
of m-dimensional currents on ℝn is a real vector space with operations defined by
Multiplication by a constant scalar represents a change in the multiplicity of the surface. In particular multiplication by −1 represents the change of orientation of the surface.
Much of the theory of distributions carries over to currents with minimal adjustments. For example, one may define the support of a current T as the complement of the biggest open set U such that T(ω) = 0 whenever the support of ω lies entirely in U.
The linear subspace of 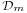 consisting of currents with compact support is denoted
consisting of currents with compact support is denoted 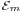 . It can be naturally identified with the dual space to the space of all smooth m-forms on ℝn.
. It can be naturally identified with the dual space to the space of all smooth m-forms on ℝn.
Homological theory
Integration over a compact rectifiable oriented submanifold M (with boundary) of dimension m defines an m-current, denoted by ![[[M]]](/2012-wikipedia_en_all_nopic_01_2012/I/c8a80646c2a3dc3c3c7cdbee3952e656.png) :
:
If the boundary ∂M of M is rectifiable, then it too defines a current by integration, and one has Stokes' theorem:
This relates the exterior derivative d with the boundary operator ∂ on the homology of M.
More generally, a boundary operator can be defined on arbitrary currents
by dualizing the exterior derivative:
for all compactly supported (m−1)-forms ω.
Topology and norms
The space of currents is naturally endowed with the weak-* topology, which will be further simply called weak convergence. A sequence Tk of currents, converges to a current T if
It is possible to define several norms on subspaces of the space of all currents. One such norm is the mass norm. If ω is an m-form, then define its comass by
So if ω is a simple m-form, then its mass norm is the usual L∞-norm of its coefficient. The mass of a current T is then defined as
The mass of a current represents the weighted area of the generalized surface. A current such that M(T) < ∞ is representable by integration over a suitably weighted rectifiable submanifold. This is the starting point of homological integration.
An intermediate norm is Whitney's flat norm, defined by
Two currents are close in the mass norm if they coincide away from a small part. On the other hand they are close in the flat norm if they coincide up to a small deformation.
Examples
Recall that
so that the following defines a 0-current:
In particular every signed regular measure  is a 0-current:
is a 0-current:
Let (x, y, z) be the coordinates in ℝ3. Then the following defines a 2-current (one of many):
See also
References
- de Rham, G. (1973) (in French), Variétés Différentiables, Actualites Scientifiques et Industrielles, 1222 (3rd ed.), Paris: Hermann, pp. X+198, Zbl 0284.58001.
- Federer, Herbert (1969), Geometric measure theory, Die Grundlehren der mathematischen Wissenschaften, 153, Berlin–Heidelberg–New York: Springer-Verlag, pp. xiv+676, ISBN 978-3540606567, MR0257325, Zbl 0176.00801.
- Whitney, H. (1957), Geometric Integration Theory, Princeton Mathematical Series, 21, Princeton, NJ and London: Princeton University Press and Oxford University Press, pp. XV+387, MR0087148, Zbl 0083.28204.
- Lin, Fanghua; Yang, Xiaoping (2003), Geometric Measure Theory: An Introduction, Advanced Mathematics (Bejing/Boston), 1, Bejing/Boston: Science Press/International Press, pp. x+237, ISBN 978-1-57146-125-4, MR2030862, Zbl 1074.49011
This article incorporates material from Current on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
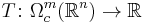
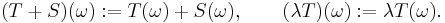
![[[M]](\omega)=\int_M \omega.\,](/2012-wikipedia_en_all_nopic_01_2012/I/cc4c5ec88999272a0e68f077f94e729a.png)
![[[M]](d\omega)=\int_M d\omega=\int_{\partial M}\omega = [[\partial M]](\omega).](/2012-wikipedia_en_all_nopic_01_2012/I/0893e6734aa3b5e3dbbde366bc8839bd.png)